T-tests explained: what they mean for survey analysis
Are there statistically significant differences in your data?
Analyzing survey results is sometimes more involved than simply comparing bar graphs.
While anyone can see the difference between two numbers, finding out whether that difference is actually statistically significant can take a little more work.
Let’s say you’ve run a customer satisfaction survey for your company, and you’ve got loads of results to analyze. You ask your boss what to analyze first and she says she wants to know if men and women give different responses. For example, do men on average give your company a lower Net Promoter Score℠ (NPS) than women?
When you dig into the data, you see that the average rating from male respondents was 9, compared to an average score of 12 from female respondents. How do you know if 9 is significantly different from 12? That’s where the t-test comes in.
The t-test is a way to determine whether two numbers are significantly different from one another. There are several types of t-test, and each is calculated using a different formula.
The three most common types of t-test
1. One-sample t-test: This test looks at whether the mean (aka average) of data from one group (in this case the overall NPS) is different from a value you specify.
Example: Your company’s goal is to have an NPS that’s significantly higher than the industry standard of 5. Your company’s latest survey puts its NPS at 10. Is an NPS of 10 significantly higher than the industry standard of 5?
2. Two-sample t-test: This test examines whether the means of two independent groups are significantly different from one another.
Example: Your hypothesis is that men give your company a lower NPS than women.The average NPS from male respondents is 9, while the average score from women is 12. Is 9 significantly different from 12?
3. Paired t-test: This test is for when you give one group of people the same survey twice. A paired t-test lets you know if the mean changed between the first and second survey.
Example: You surveyed the same group of customers twice: once in April and a second time in May, after they had seen an ad for your company. Did your company’s NPS change after customers saw the ad?
Note that while t-tests can tell you if something is significantly different, it’s up to you to determine whether that difference is meaningful. Small differences can be statistically different if the sample size is large enough.
How to conduct a t-test
There are 4 steps to conducting a t-test:
1. Calculate the t-statistic:
Each type of t-test has a different formula for calculating the t-statistic (You can scroll to the bottom of the page to find all three formulas).
2. Calculate the degrees of freedom:
Degrees of freedom are the number of ways the mean could vary. In this case, the degrees of freedom are the number of NPS ratings that you could have in a given group of respondents. Similar to the t-statistic, the formula for degrees of freedom will vary depending on the type of t-test you perform.
3. Determine the critical value:
The critical value is the threshold at which the difference between two numbers is considered to be statistically significant.
4. Compare absolute value of the t-statistic to critical value:
If your t-statistic is larger than your critical value, your difference is significant. If your t-statistic is smaller, then your two numbers are, statistically speaking, indistinguishable.
Pulling it all together
Let’s walk through the example from the beginning: Your hypothesis is that men give a lower NPS to your company than women. The average NPS from men is 9, while the average score for women is 12. Is 9 significantly different from 12? This is an example of where to use the two-sample t-test.
1. Calculate t-statistic:
Below is the formula for the two-sample t-test, where:
- t is the t-statistic
- x1 is the average NPS for men → 9
- x2 is the average for women → 12
- n1 is the number of men who provided a response to the NPS question → say 20 men responded to the survey
- n2 is the number of women → 23 women responded
- s1 is the standard deviation of the NPS for men → say the calculated standard deviation is 12.48
- s2 is the standard deviation of the NPS for women → the calculated standard deviation is 10.51
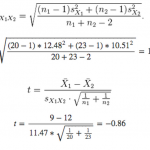
2. Calculate the degrees of freedom:
This formula must be used to determine degrees of freedom in two-sample t-tests. The formulas for other types of test are included below.

3. Determine critical value:
According to this table, for a two-tailed test with an alpha level of 0.05 at 41 degrees of freedom, the critical value is 2.02. Note that most analysts use a two-tailed test instead of a one-tailed test because it’s more conservative. For more information on the differences between one-tailed and two-tailed tests, check out this video from Khan Academy.
4. Compare absolute value of the t-statistic to critical value:
Since the absolute value of the t-statistic is 0.86, which is not larger than the critical value of 2.02, then you can conclude that men do not give a significantly lower NPS ratings than women.
Formulas for other t-tests
You’ll probably be conducting the t-tests in a spreadsheet or statistical program (like Excel or SPSS), but if you’d like to do the math by hand, the formulas for the other two types of t-tests are included below.

If you decide (as most people do) to conduct t-tests in a spreadsheet or statistical program, the process will be slightly different. Instead of comparing the t-statistic to the critical value, most programs calculate a p-value, which it compares to your alpha level (the most commonly used level is 0.05). In this case, a p-value lower than your alpha level will show that the numbers are significantly different.
Net Promoter Score is a trademark of Bain & Company, Inc., Satmetrix Systems, Inc. and F. Reichheld.
Discover more resources

Toolkits Directory
Discover our toolkits, designed to help you leverage feedback in your role or industry.

Get feedback you can act on with online evaluation forms
Unlock the power of feedback with SurveyMonkey's online evaluation forms. Start with our form builder today!

Survey Best Practices
Learn our survey best practices to make the most of your next survey. Explore our survey guidelines and get started today, for FREE!

Collect key contact information with online contact forms
Create customisable contact forms and easily add them to your website. Or use one of our pre-filled templates to grow your business faster.